LCフィルタを含むモーターの伝達関数

初めに

前回の記事はこちらです。

ここではHブリッジ回路で使用した負荷側の伝達関数の導出を行ってみます。

回路図

回路図概要

下記に回路図を記載します。

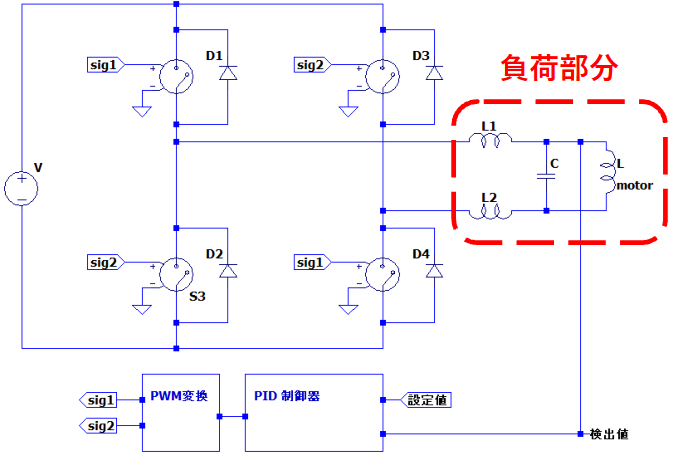
上図の赤い点線の部分の負荷のラプラス変換を行っていきます。

赤い部分の図を抽出するとモーター負荷を含めた回路図は下記の通りになります。

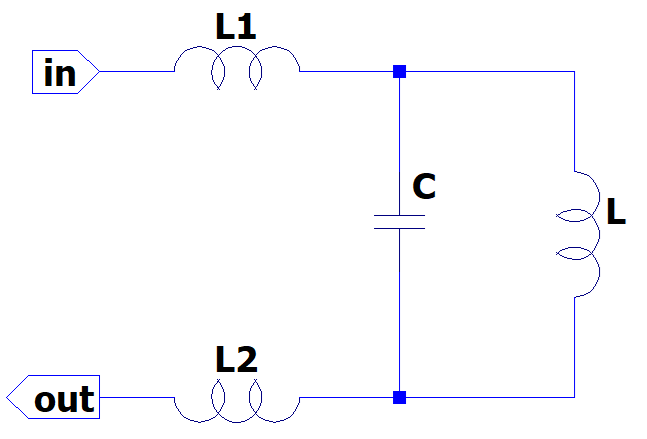
上記の図を元にラプラス変換を検討してみる。

ラプラス変換

回路図をラプラス変換した形にまとめなおすと下記の通りになる。

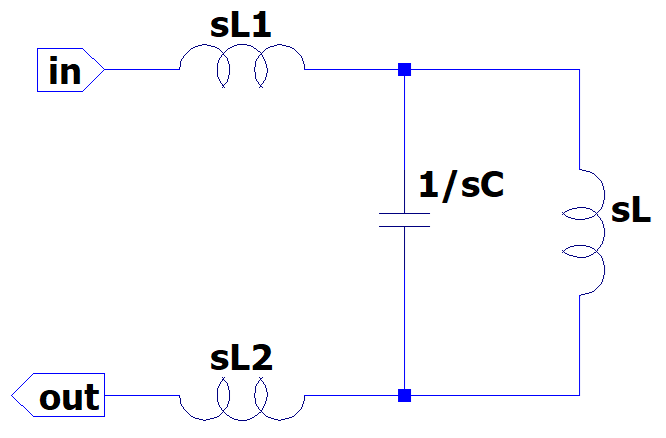
上記の回路を元にVinとVoの式の形にする為に回路図を調整すると

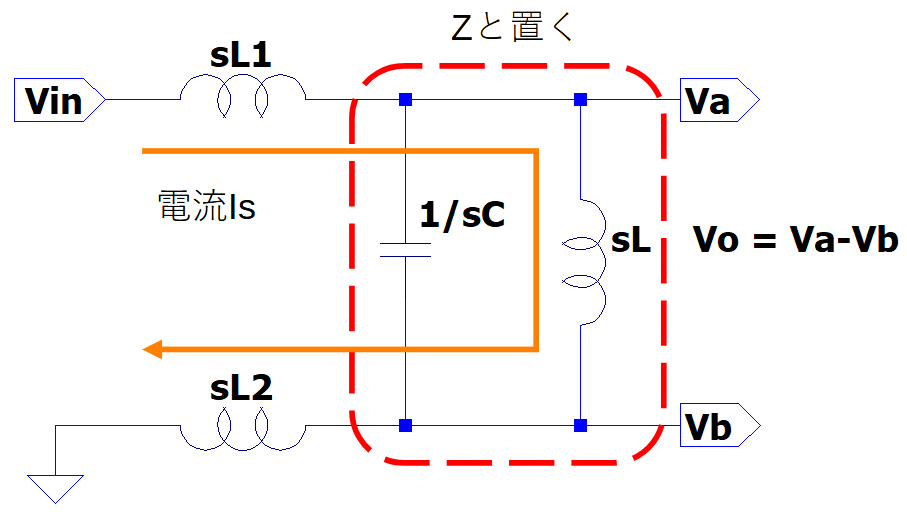
この図の通りになる。この図を元に式を計算してみる。

式まとめ

上図を元に式を立てると下記の通りになる。

1. 入力電圧\(\rm{V_{in}}\) = \(\rm{sL_{1}}\)\(\rm{I_{s}}\) + \(\rm{Z}\)\(\rm{I_{s}}\) + \(\rm{sL_{2}}\)\(\rm{I_{s}}\)・・・(1)
2. 出力電圧\(\rm{V_{o}}\) = \(\rm{Z}\)\(\rm{I_{s}}\)・・・(2)
3. インピーダンス\(\frac{1}{\rm{Z}}\) = \(\rm{sC}\)+\(\frac{1}{\rm{sL}}\) ・・・(3)

式(3)を計算すると、下記の通りになります。

4. インピーダンス\(\rm{Z}\) = \(\frac{sL}{s^{2}LC+1}\) ・・・(4)

ここで、式(1)、式(2)を元に\(\rm{V_{o}}\)と\(\rm{V_{in}}\) をまとめると下記の通りになります。

5. 出力電圧\(\rm{V_{o}}\) = \(\frac{Z}{\rm{sL_{1}}+\rm{sL_{2}}+\rm{Z}}\) \(\rm{V_{in}}\)・・・(5)

式(5)に式(4)を代入し、式をまとめると下記の通りになります。

5. 出力電圧\(\rm{V_{o}}\) = \(\frac{\frac{1}{\rm{C}(\rm{L_{1}+L_{2}})}}{\rm{s^{2}} + \frac{\rm{L}+\rm{L_{1}}+\rm{L_{2}}}{\rm{LC}(\rm{L_{1}}+\rm{L_{2}})}}\) \(\rm{V_{in}}\)・・・(6)

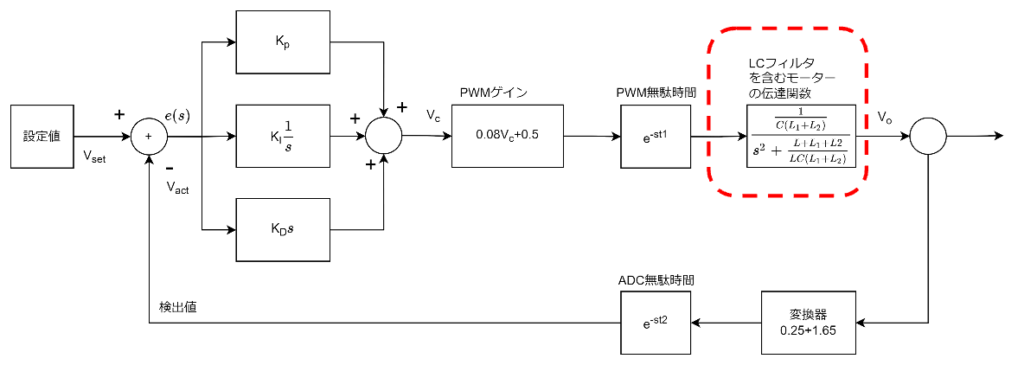
式(6)の結果がLCフィルタを入れた際の計算結果になります。これらの結果より前ページで乗せたように下記の通りのブロック図になります。

まとめ

LCフィルタを含んだ伝達関数の計算を行ってみた。こちらをもう少し検証し、実機と計算が合うか今後計算してみたい。

今後共継続して作業を進める。