初めに
※2024/12/1 図の一部を修正
本記事ではHブリッジ回路によるモーターコントロールのシミュレーション製作に関して記載致します。モータ駆動の正転反転を制御するように考えました。
今はシミュレーションだけですが、後にラズベリーパイピコを使って実際にモータの制御を行ってみたいと思います。
Hブリッジとは
概要
Hブリッジ回路とは、FETもしくはトランジスタをHの字型に組んだ回路構造の事を指し、負荷に対する出力の正負を反転する動作をさせる事が出来る回路になります。
ざっくりとしたイメージは下記の通りになります。
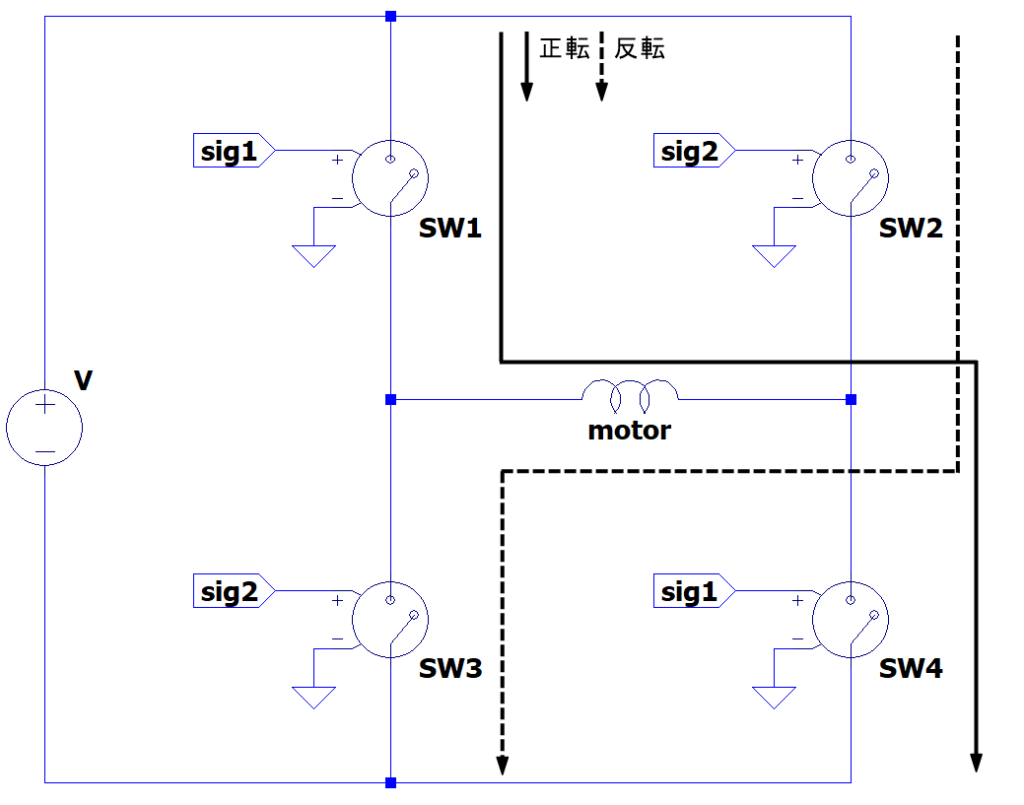
SWをH型に設置した回路になっており、SWの駆動パターンを変えることで負荷(motor)に対しての電流の向きを変えることが出来ます。
motorは流れる電流の向きで回転方向が変わる為、この作用によってmotorを正転、反転させることが可能になります。
デットタイム
Hブリッジでモータを駆動する際には、下記に示すようにSW1-3,1-4を同時に駆動すると、電源がショートしてしまい貫通電流が流れSWが壊れてしまいます。
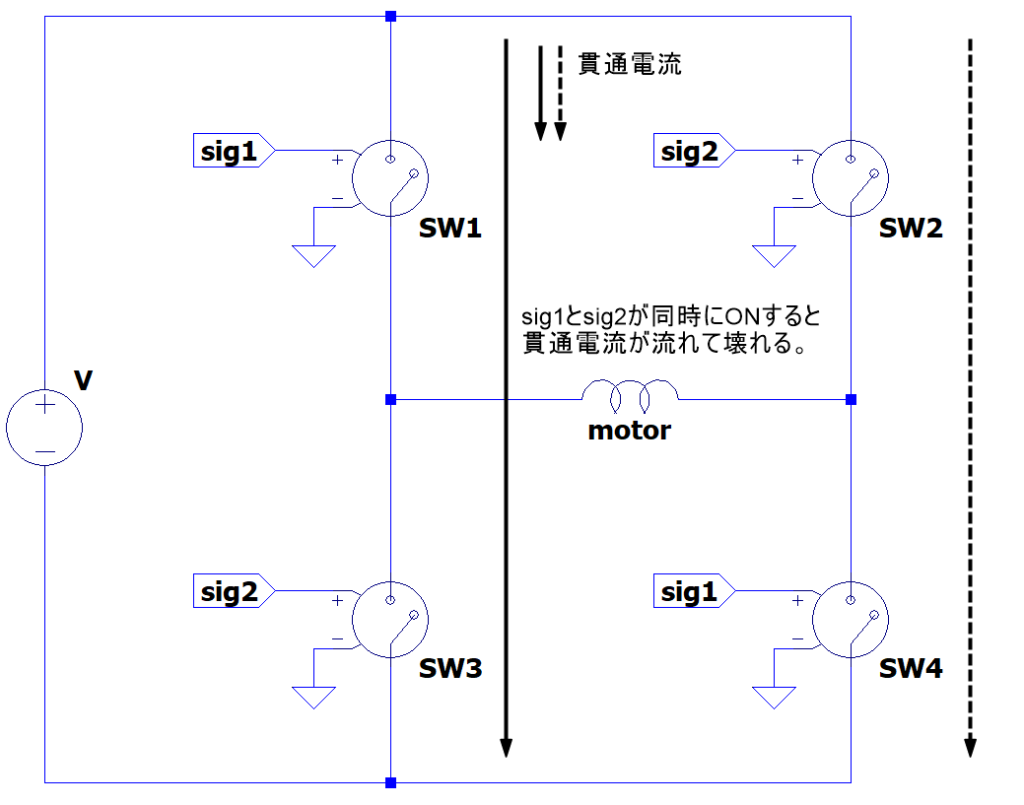
そこで下記に示すようにDeadtimeという時間を設定することで、貫通電流が流れる事を阻止する事が出来るようになります。
フライホイールダイオード(FRD)
FET等を使ったSW制御では、インダクタンスに対して出力する事があるので、FET側に逆起電力が生じたりします。その逆起電力を逃がす方法として、FRD(フライホイールダイオード)を用いた回路を使用致します。
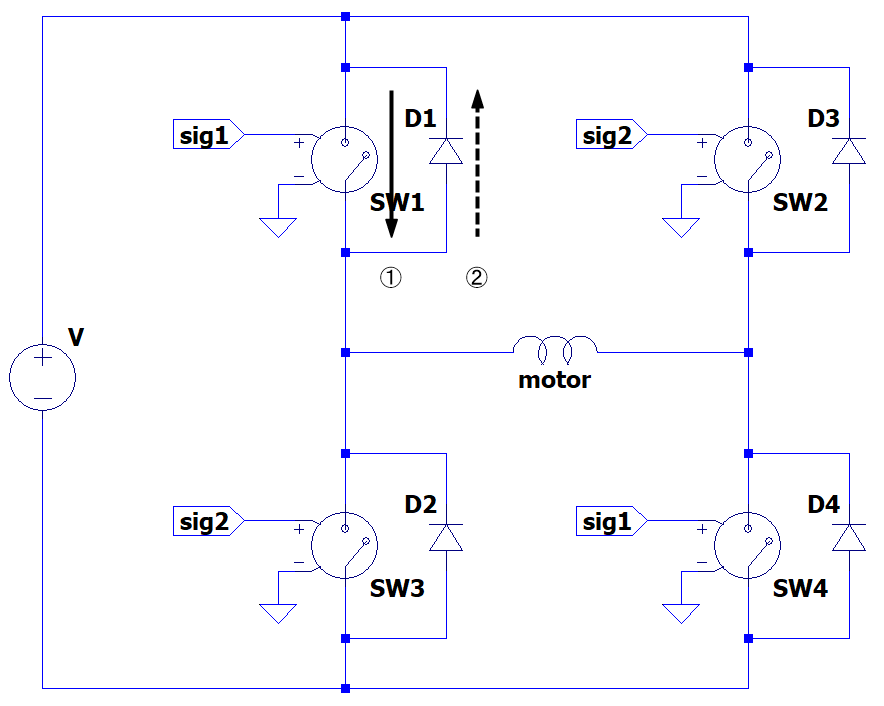
基本的に上記画像上で①に電流が流れた後に生じる逆起電力②をFRDを用いて電源側に流すことでエネルギーの逃げ道を作っております。
PWMによるコントロール
Hブリッジ回路の出力コントロールには、PWM出力を用いてコントロールを行う予定です。
PWM出力とはPulse Width Modulation(パルス幅変調)出力の事であり、下記に示すようにパルス幅の大きさを変化させる事で出力を変更する出力方式になります。
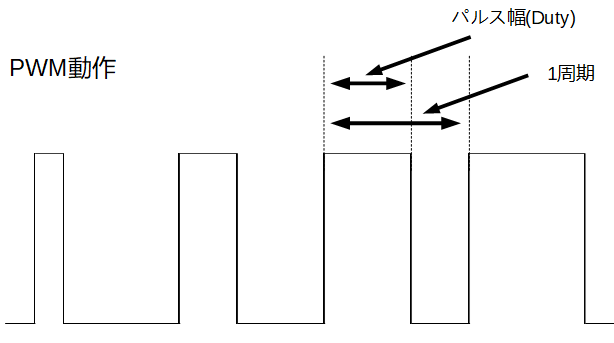
このパルス幅をDutyと呼び、1周期とパルス幅の割合をDuty比と呼ばれています。
パルス幅を制御する事で出力量を調整することが出来るようになります。
LCフィルター
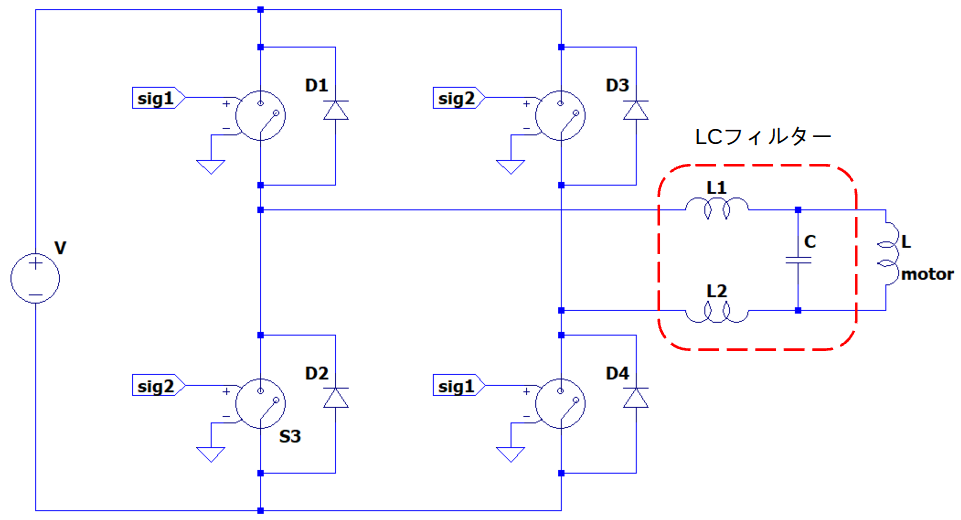
ここではPWMの出力をそのままモーターに入れてしまうと、ノイズが大きくなってしまう為、それを軽減させる為に、間にLCフィルタを入れます。LCフィルタを入れた際の回路図は下記の通りになります。
制御回路
制御回路では下記に示すPI制御器の考えを元にラズベリーパイピコを使ってPID制御器を作成致します。アナログのPI制御器はこちらを参考にしてください。(リンク)
ここで、まず機器の一般的なフィードバック制御のブロック図を下記に記載致します。

上記のブロック図は設定値と検出値の差を補償器を通して負荷に出力を行う系になります。検出値を取り込むことでフィードバック制御を行っております。
PID制御器とは、P(Propotional 比例),I(Integral 積分),D(Differential 微分)を使った制御器の事であり、上記ブロック図の補償器の部分で使用する事になります。上記ブロック図を修正すると下記の通りになります。
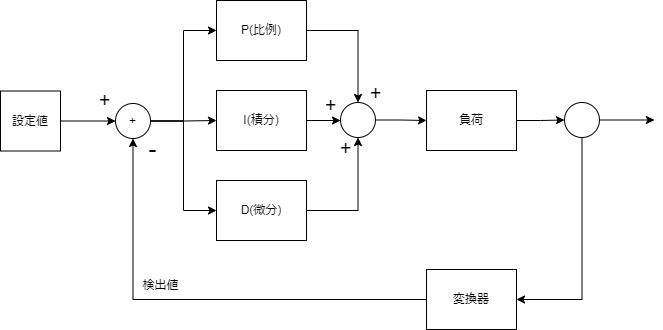
上記の図がPID制御器を用いたフィードバック系の形になります。ここで上記制御系を数式化する事を考える為に、下記のように数式を置くと、
- 設定値\(\rm{V_{set}}\)-検出値\(\rm{V_{act}}\) = \(e(t)\)・・・(1)
- P(比例) = \(\rm{K_P}\)・・・(2)
- I(積分) = \(\rm{K_I} \int dt \)・・・(3)
- D(微分) = \(\rm{K_D} \frac{d}{dt} \)・・・(4)
- 負荷 = \(\rm{RC} \)・・・(5)
- 変換器 = \( \frac{1}{\rm{X}} \)・・・(6)
となり、ブロック図に直すと以下のようになります。
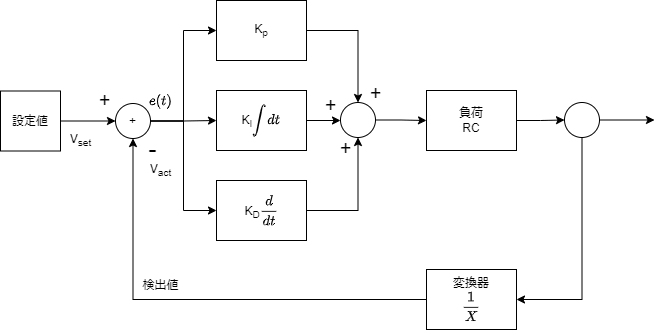
形としてはこのようになりました。このままだと計算しにくいので、ラプラス変換といったものを用いて上記のブロック図を変数sでまとめます。
ラプラス変換とは、時間関数tを周波数領域の関数sへ変換する手法の事を指します。
周波数領域関数sへ変換する事で式をまとめやすくなり、その後もう一度時間関数tの領域に戻すことで、時間関数tの式を簡単に求める事になります。
さっくりしたイメージはリンク先をご覧ください。
ここで上記ブロック図の全体をラプラス変換すると下記のようになります。
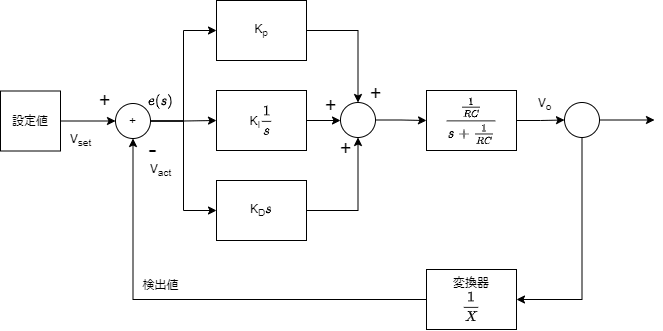
ここで負荷RFは下記の回路としました。
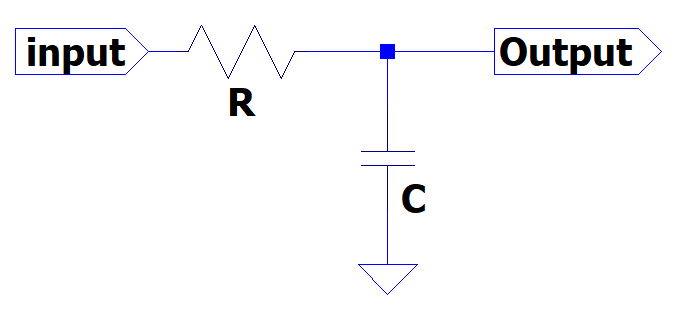
上記の図より補償器であるPID制御器は下記の式の通りになります。
$$C(s) = \rm{K_P} + \frac{\rm{K_I}}{s} + \rm{K_D} s・・・(7)$$
ここで積分ゲイン\(\rm{K_I}\)と微分ゲイン\(\rm{K_D}\)は比例ゲイン \(\rm{K_P}\) で表すと下記の通りになります。
$$\rm{K_I} = \frac{\rm{K_P}}{\rm{T_I}} ・・・(8)$$
$$\rm{K_D} = \rm{K_P}\rm{T_D}・・・(9)$$
\(\rm{T_I}\)、\(\rm{T_D}\)はは積分時間、積分時間と言われ、比例制御に対してどのくらい積分時間、微分時間が必要か系を確認してパラメータを設定する。 ここで式(7)に式(8)、式(9)を入れると下記の通りになります。
$$C(s) = \rm{K_P}(1+ \frac{1}{\rm{T_I}s} + \rm{T_D} s)・・・(10)$$
式(10)がPID制御の基本式ではあるんですが、微分項目はこのままつかうと反応が過敏すぎてハンチングの原因になってしまいます。
そこで不完全微分形式にする事である程度の電圧変動では反応しないようにすることが出来ます。不完全微分型の式を入れてPIDの式をまとめると
$$C(s) = \rm{K_P}(1 + \frac{1}{\rm{T_I}s} + \frac{\rm{T_D}s }{1+\rm{nT_D}s})$$
となります。この式は微分項に関して1次の遅れフィルタの\(\frac{1}{1+\rm{nT_D}s}\)を入れて、急峻な応答をゆるやかにとらえるように調整した式になります。(nはゲイン係数で、通常0.1~0.125程度の値を入れます。)
電圧制御によるコントロール
上記の結果を踏まえて、PID制御を入れたHブリッジ回路のブロック図を修正してみます。そうすると下記の図の通りになります。
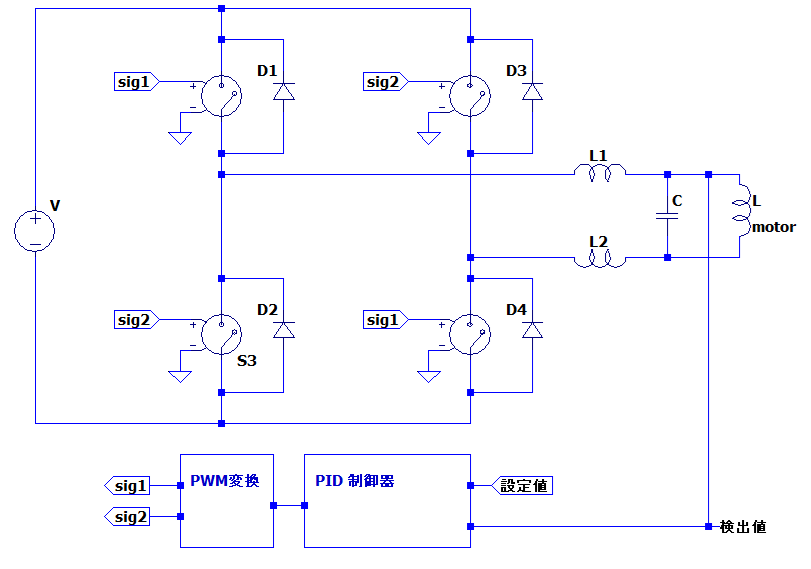
ひとまず電圧制御のほうが難しくないので、電圧制御でモータのコントロールを行う事にしました。モーターの片側の電圧を検出値として設定値と検出値を比較してPID制御器を介してPWMの出力を行います。ラズベリーパイピコにはPWM出力機能があるので、ラズベリーパイピコでPID制御器とPWM変換の部分を作成しようと思います。
上記のブロック図を制御ブロック図に直すと下記の通りになります。
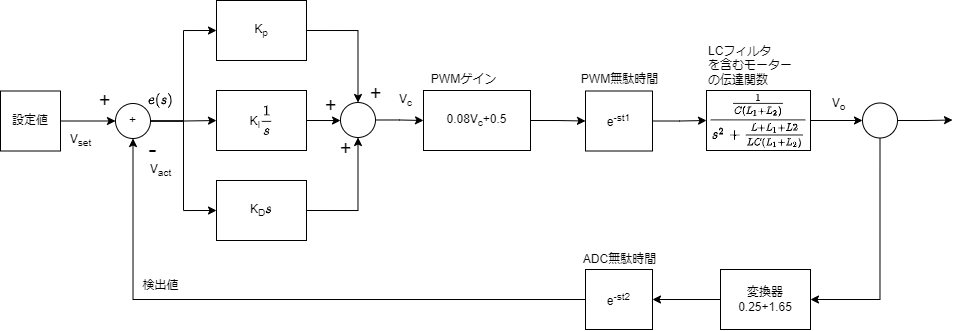
構成としては、設定部分、PID制御器、PWM出力部+無駄時間、LCフィルタとモータ(負荷)、検出部(変換器)+ADCの無駄時間の構成となっております。
PWMのゲインは、PIDの出力を90%Duty時5V、10%Duty時を-5Vの出力として計算しました。また変換器に関しては、DCモーターの定格出力±6Vを0~3.3Vに落とし込んだ値としております。
PWM出力は1周期1msとしているので、計算もその間に終わると仮定し、無駄時間も1周期遅れの1msとしております。ADCの無駄時間はサンプリングタイムの2usとします。
LCフィルタを含むモーターの伝達関数の導出に関しては長くなるので別途記事に致します。伝達関数の計算はこちらの記事になります。
今回使用するモーターとしてはプラスチックギアードモーターであるHP-08-13047-8を想定してみます。インダクタンス値等の情報がなかったので、シミュレーションの際は仮で仮定してシミュレーションします。
LTspiceによるシミュレーション
LTspiceを用いて下記の回路図のシミュレーションを行った。制御器としては、ひとまずアナログの制御器を用いて行った。
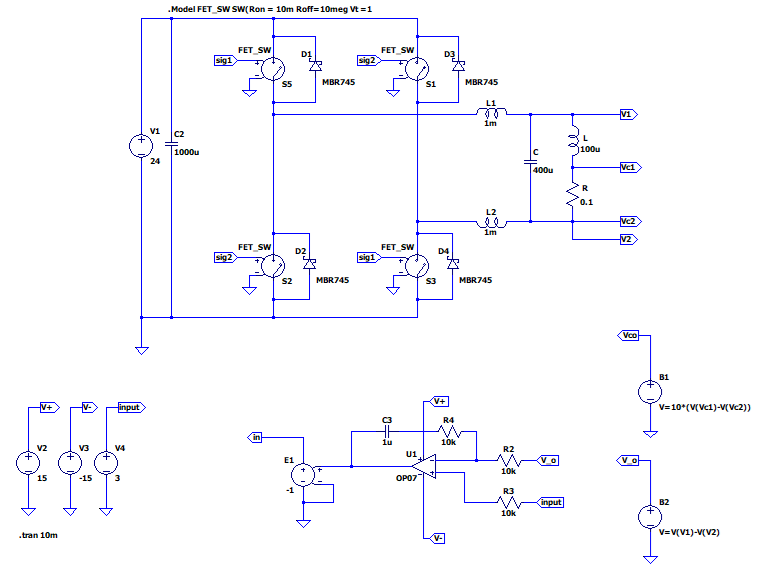
Voの出力結果を下記に記載する。20ms程度ハンチングが生じているが、6Vで制御出来ていることが分かります。
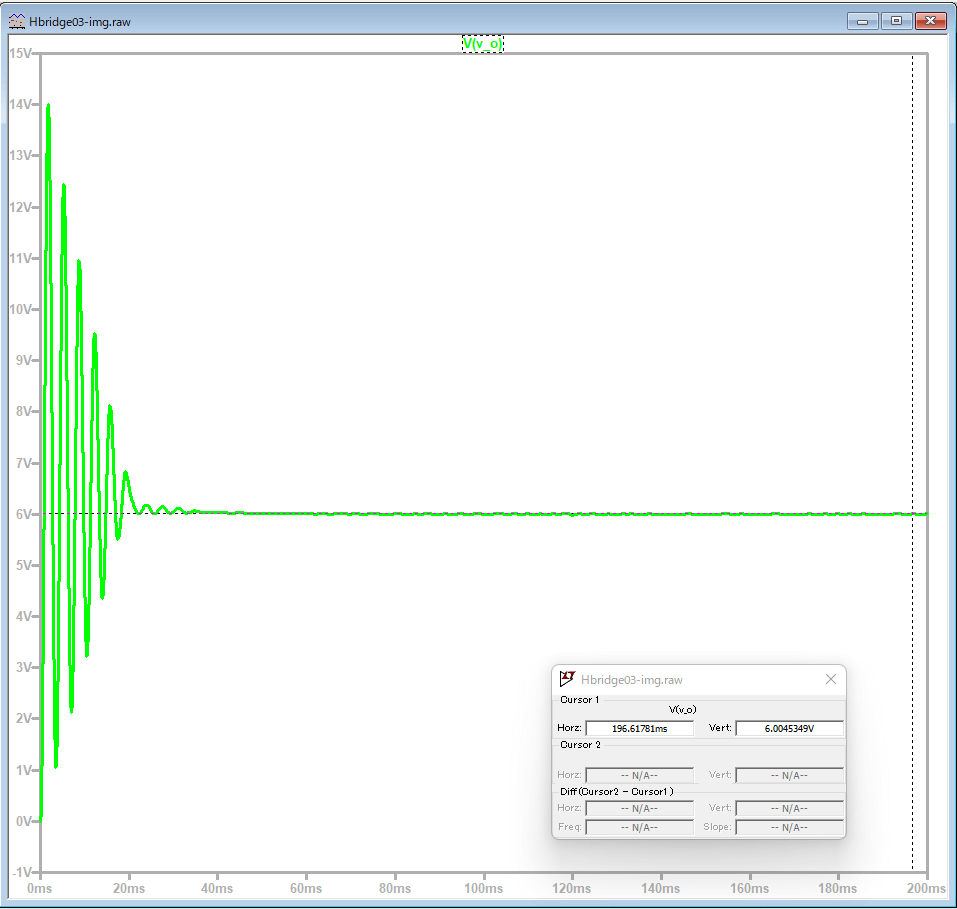
これでHブリッジを用いてのモーターの電圧制御が出来ることが確認出来た。上記のシミュレーション以外にも-6Vでも出力出来ることは確認出来た。
まとめ
ひとまずHブリッジを使ってモーターのコントロールが出来ることがシミュレーション出来た。上記の結果を用いて実際にモータの駆動が出来るか実践していきたいと思います。



コメント